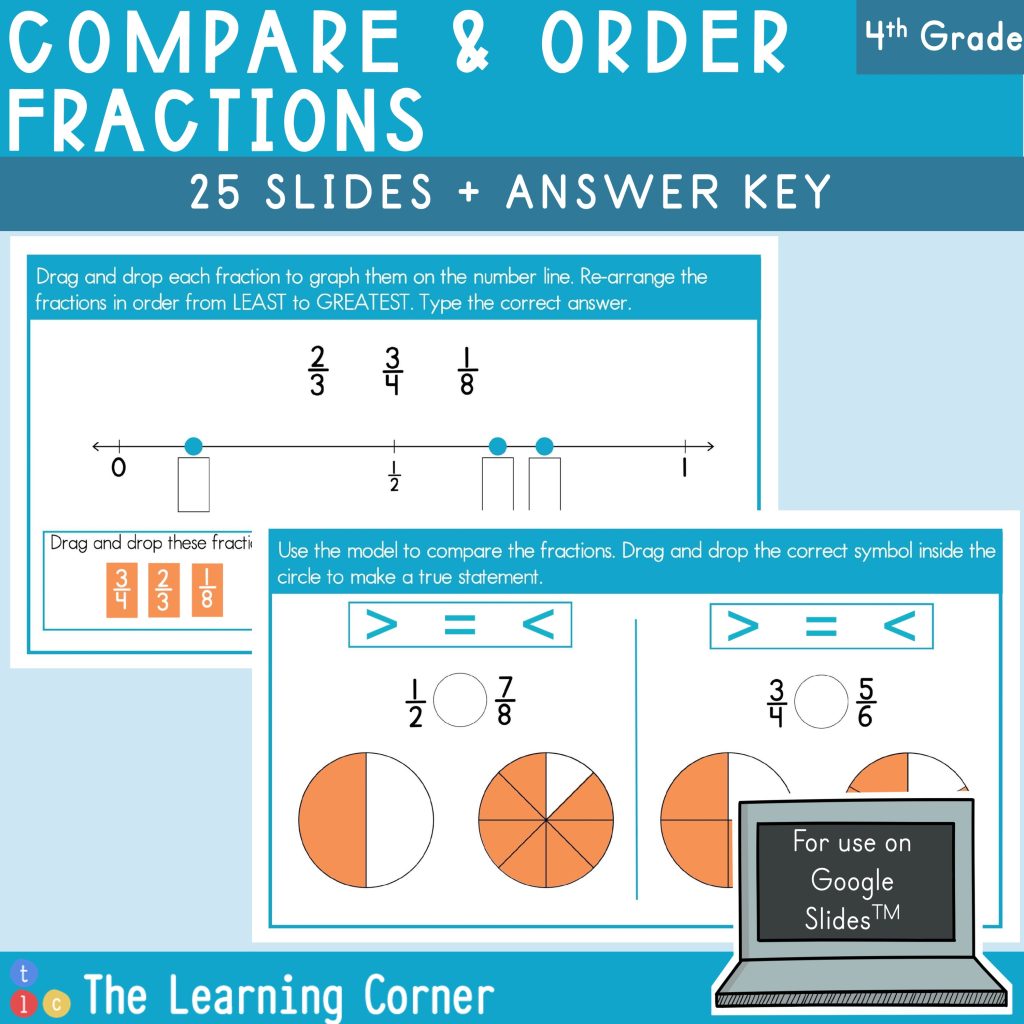
Comparing fractions can be tricky, but using models and strategies will help students understand the concept a lot easier.
First, let’s review what a fraction is. A fraction represents part of a whole. It shows two numbers separated by a horizontal bar. The number on top called the numerator represents the number of pieces or parts being counted. The number at the bottom called the denominator represents the number of pieces or parts a whole has.
Let’s look at this word problem as an example. A pizza is divided into 8 equal slices. Your family eats 3 slices of them. What fraction represents the part that was eaten?
Since you are counting the number of parts eaten, then your numerator should be 3. Since the pizza has 8 slices, then your denominator should be 8. The amount of pizza that you’ve eaten is three-eighths (3/8).
Comparing Fractions With Same Denominators
Now, let’s look at some ways to compare fractions. One way to compare fractions is by using common denominators. Fractions have common denominators when the bottom numbers are the same number. When comparing fractions with the same denominator, the fraction with the bigger numerator is the greater fraction. This is because when fractions have the same denominators, the more pieces or parts a fraction has, the bigger the fraction is.
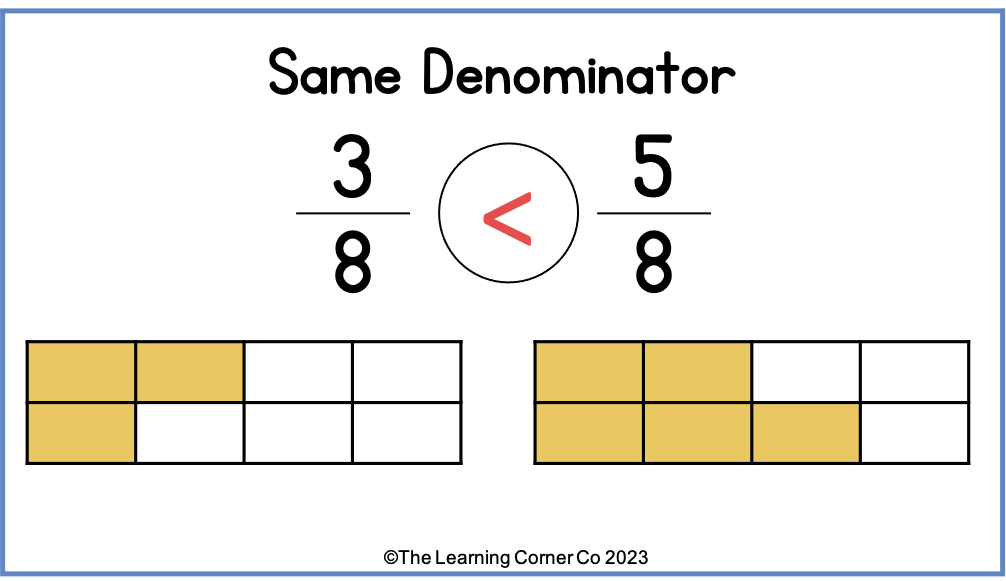
For example, let’s compare 3/8 (three-eighths) and 5/8 (five-eighths). These two fractions have the same denominator. Since these two fractions have the same denominator, we can compare their numerators.In this example, since 3 is less than 5, we know that 3/8 is less than 5/8.
Comparing Fractions Using Same Numerators
Another way to compare fractions is by using common numerators. Fractions have common numerators when they have the same number on top. When comparing fractions with the same numerator, the fraction with the smaller denominator is the greater fraction. This is because the smaller the denominator is, the bigger the pieces are.
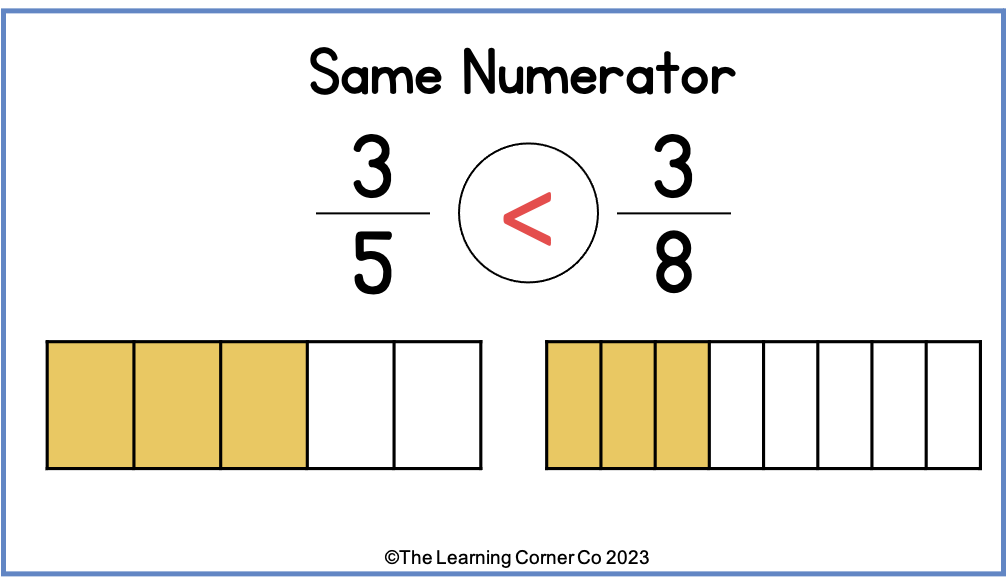
For example, let’s compare 3/5 and 3/8. These two fractions have the same numerator. Since these two fractions have the same numerator, we can compare their denominators. In this example, since 5 is less than 8, 3/5 is greater than 3/8.
Compare Fractions with Unlike Denominators
What if your fractions don’t have the same numerator or denominator? Then, we can write the fractions so that they have a common denominator. For example, compare 3/5 and 2/3. These fractions don’t have the same numerator or denominators. What you can do is to find the least common multiples of 3 and 5 which is 15. Rewrite the fractions 3/5 and 2/3 as 9/15 and 10/15. Now that they have a common denominator, you can compare the numerators. Since 9 is less than 10, 9/15 or 3/5 is less than 10/15 or 2/3.
Activities to Practice Comparing Fractions
Now that we know several strategies to compare fractions, let’s look at some examples and activities that you can use in the classroom or at home to help students understand and practice the concept.
- Use fraction word problems. Create word problems that involve comparing fractions. For example: Jackie ate one-half of a lasagna. Her brother, ate one-fourth. Who ate more lasagna?
- Use models such as fraction tiles and number lines. Write comparison problems on index cards and have students use fraction tiles or numbers lines to compare the fractions.
Join my email list to get these Comparing Fractions Task Cards!
- Use worksheets and online resources. Worksheets and resources are great independent practice for students. Check out some of my TPT resources below.
By using these strategies and activities, students will have a better understanding of how to compare fractions.