An area model is a powerful visual tool for a better understanding of how division works. In this blog post, you will have a guide on how to use area models to divide with remainders and without remainders.
Need to know how to use area models to multiply? Check out this blog post.
What are Area Models?
Before we start dividing using area models, let’s see what area models are. Area models are rectangular diagrams. They are used in math to solve multi-digit division problems.
Area models are helpful to breakdown the dividend into smaller numbers. Instead of having a huge number to divide, think in multiples of the divisor! This will make it easier for you to divide.
How do you do area model division without remainder?
Now, let’s see. How do you divide using area models?
When using area models to divide, you can follow these steps.
- Draw a rectangle.
- Write the dividend next to the left side of the rectangle.
- Think of a number that you can multiply by the divisor to get to the dividend without getting over. (Hint: Multiples of 10 are easy to divide by!) Write that number on top! These are your partial quotients.
- Subtract the multiple of the divisor from the dividend.
- Repeat steps 3 and 4 until the difference is 0 or less than the divisor.
- Add the partial quotients (the numbers on top of the rectangle).
Example 1: 2-Digit by 1-Digit Division
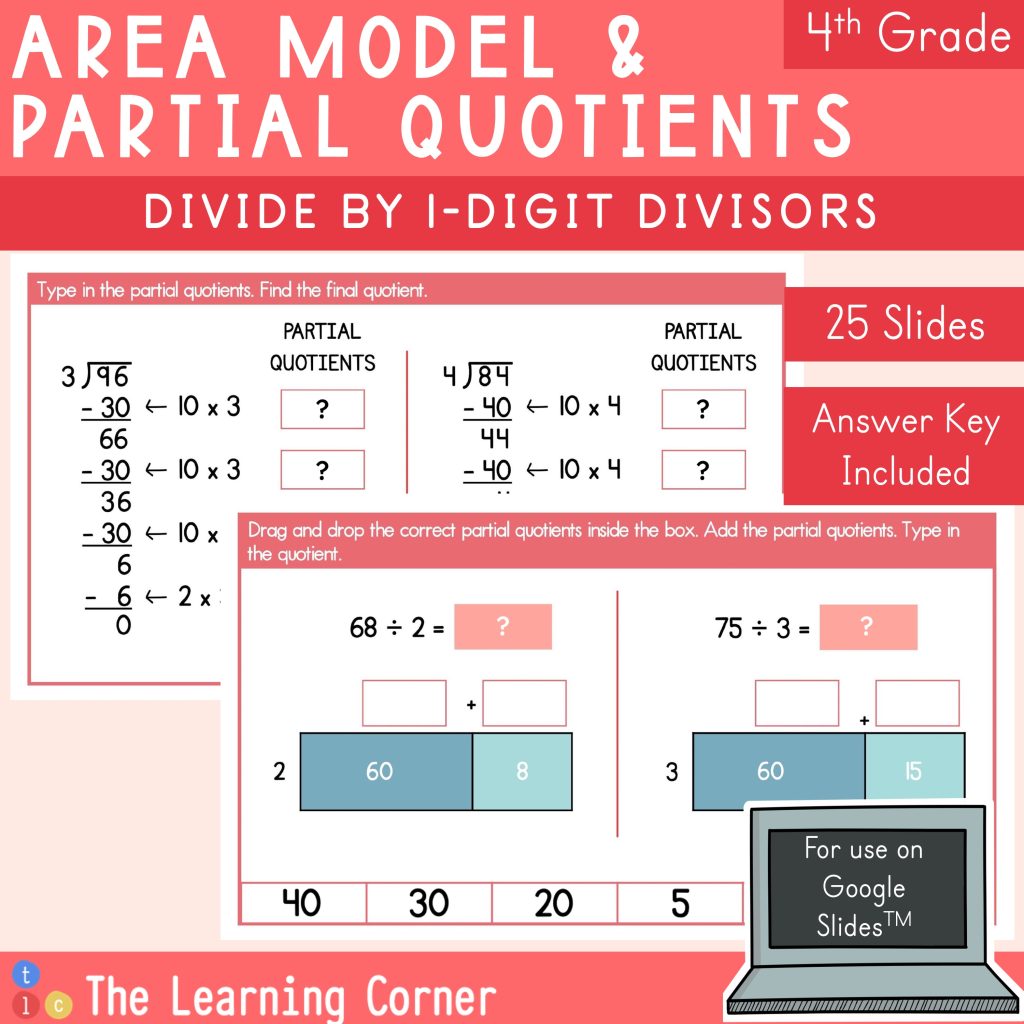
Let’s divide 48 ÷ 3.
Draw a rectangle.
Write 48 next to the left side of the rectangle.
Now, think: What number can I multiply by 3 that can make 48 or less? (Think in 10s!)
3 x 10 = 30
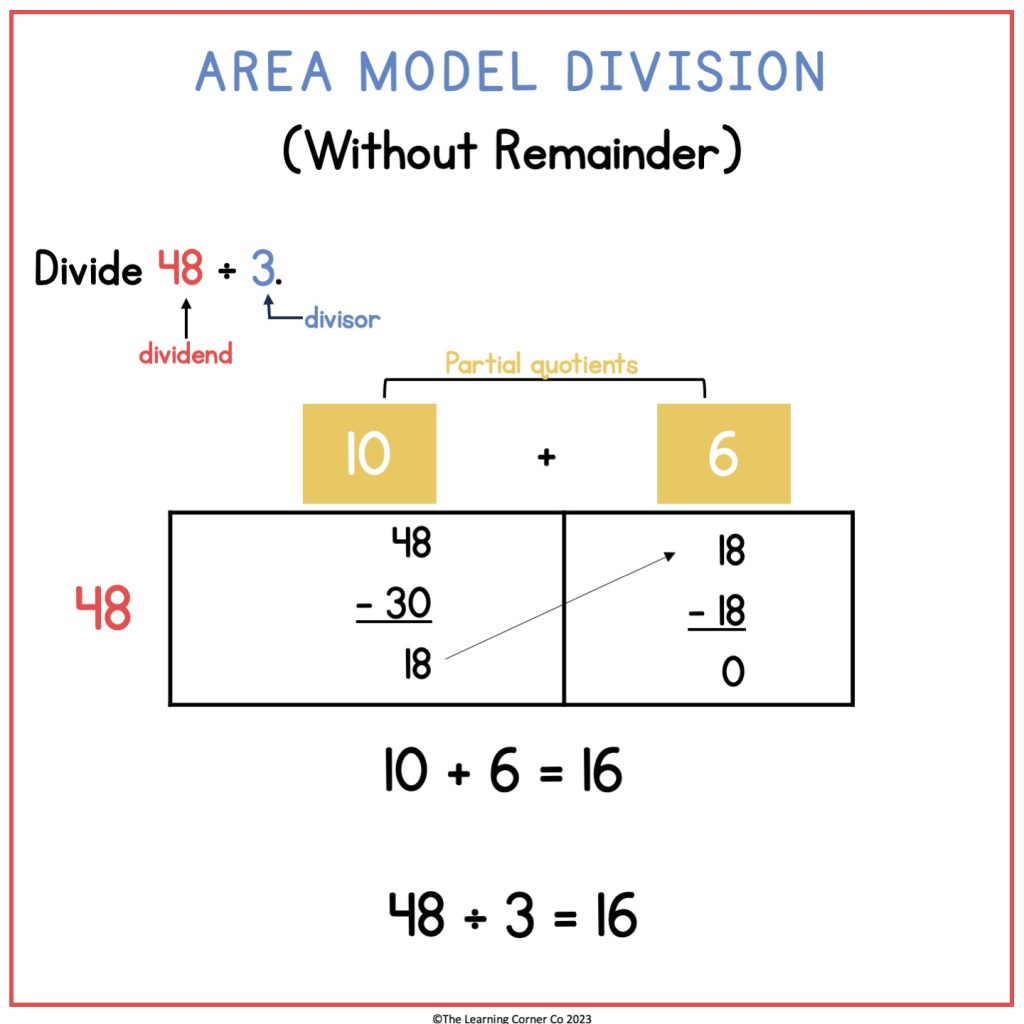
Write 10 on top of the rectangle and subtract 30 from 48.
48 – 30 = 18
Now, you are left with 18. Draw a vertical line to split the rectangle and show that you still have 18 left.
Then, you have to think again: What number can I multiply by 3 to make 18?
3 x 6 = 18
Write 6 on top of the rectangle just right above 18. Subtract 18 from 18.
18 – 18 = 0.
Since you have 0 left, you can now add the partial quotients (the numbers on top of the rectangle).
10 + 6 = 16
So, 48 ÷ 3 = 16
Example 2: 3-Digit by 1-Digit Division
Let’s work our way up to 3-digit numbers.
Divide 144 ÷ 6.
Draw a rectangle and write 144 next to the left side of the rectangle.
Now, think: What number can I multiply by 6 so that I can make 144 or less? Here, we can use 20.
6 x 20 = 120.
Write 6 on top of the rectangle. Subtract 120 from 144.
144 – 120 = 24
Draw a vertical line to split the rectangle and show that you have 24 left.
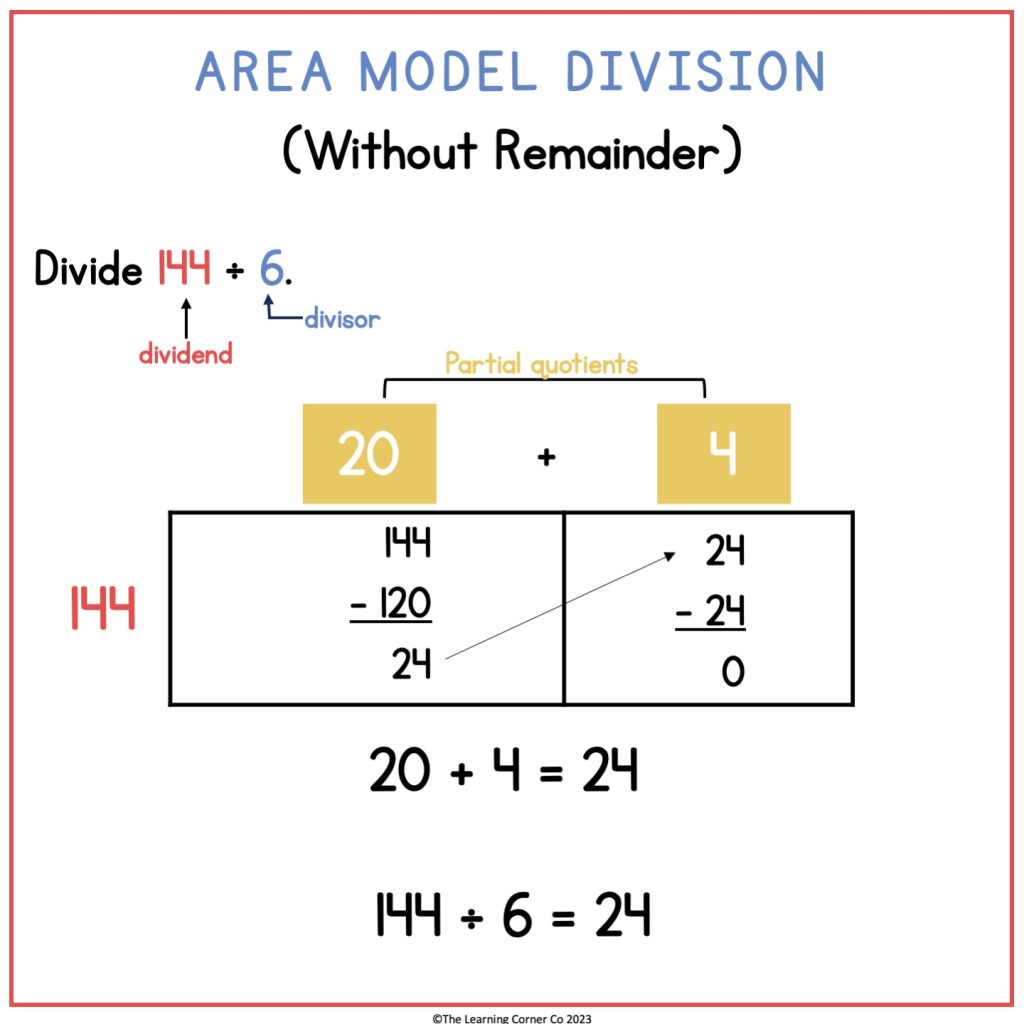
Think again, what number can I multiply by 6 to make 24 or less?
6 x 4 = 24
Write 4 on top of the rectangle just right above 24. Subtract 24 from 24.
24-24 = 0.
Add the partial quotients.
20 + 4 = 24
That means that 144 ÷ 6 = 24.
So that is how you can divide multi-digit numbers using area models.
How do you do Area Model Division with Remainders?
Now, how do you divide with remainders using area models?
Follow the same steps as when dividing without remainders but make sure to write the remainder.
- Draw a rectangle.
- Write the dividend next to the left side of the rectangle.
- Think of a number that you can multiply by the divisor to get to the dividend without getting over. (Hint: Multiples of 10 are easy to divide by!) Write that number on top! These are your partial quotients.
- Subtract the multiple of the divisor from the dividend.
- Repeat steps 3 and 4 until the difference is 0 or less than the divisor.
- Add the partial quotients (the numbers on top of the rectangle).
- Write the remainder.
Example: Division with Remainders using Area Models
Let’s look at this example. Divide 128 ÷ 5.
Draw a rectangle. Write 128 next to the left side of the rectangle.
Think, what can I multiply by 5 so that I can make 128 or less?
5 x 20 = 100
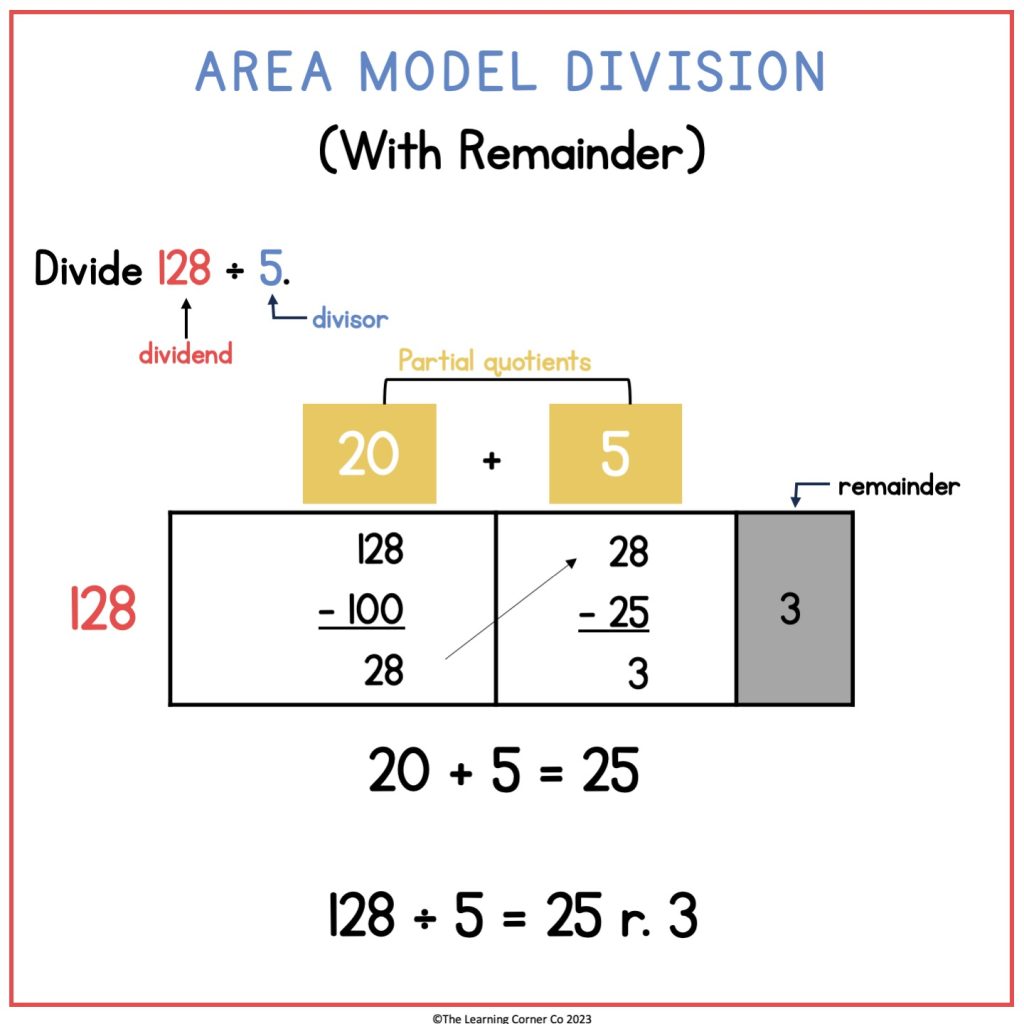
Write 20 right above the rectangle. Subtract 100 from 128.
128 – 100 = 28
Draw a vertical line to split the rectangle and show that you have 28 left.
Now, think: What number can I multiply by 5 so that I can make 28 or less?
5 x 5 = 25
Write 5 right above 28. Subtract 25 from 28.
28 – 25 = 3
Now, you have 3 left. Think, can I still make a group of 5 when given 3? No, I don’t think so! This means that 3 is your remainder.
Lastly, add the partial quotients.
20 + 5 = 25
So, 128 ÷ 5 = 25 r. 3
That’s it! You should already know how to divide using area models.
Check out these worksheets and digital activities to help you practice area model division.