Area model multiplication is a great strategy when learning multi-digit multiplication. They help break down the numbers into easy-to-multiply digits and make multiplying friendly. In this article, you will learn how to use an area model to multiply 2-, 3-, and 4-digit numbers by 1-digit numbers and 2-digit numbers by 2-digit numbers.
Area Model Multiplication: 2-, 3-, and 4-Digit Numbers by 1-Digit Numbers
The most important thing to remember about area model multiplication is that you need to break down the numbers so that it is easier to multiply them. Other than having smaller chunks of numbers to multiply, it also helps visualize the process of multiplication.
Multiply 2-digit by a 1-digit number
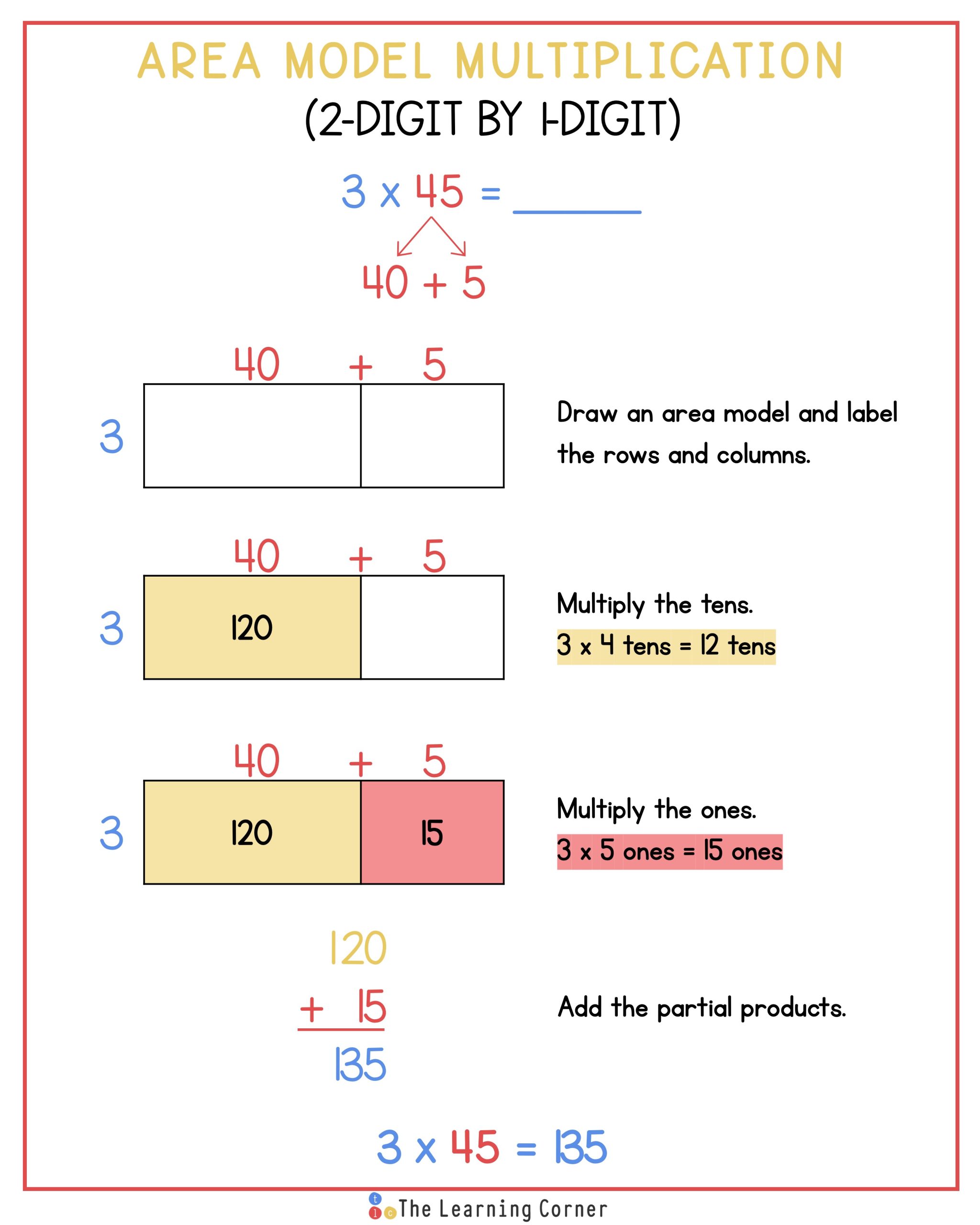
In order to use an area model to multiply by 1-digit numbers, break down the other factor first. For example, you are multiplying 3 x 45. Break down 45 so that it shows tens and ones.
45 = 4 tens 5 ones or 40 + 5
Next, draw a rectangular model and split the model into two so that one part of the rectangle is slightly bigger than the other. This will help show that the tens part is greater than the ones part.
Third, on the top part of the rectangle, label the bigger part as 40 and the smaller part as 5.
Next, label the left side of the rectangle as 3.
Now you’re ready to multiply. First, multiply the tens. Write the product inside the box directly below 40.
4 tens x 3 or 40 x 3 = 120
Then, multiply the ones. Write the product inside the cell directly below 5.
5 ones x 3 or 5 x 3 = 15
Then, add the products.
120 + 15 = 135
This means that the product of 3 x 45 is 135.
Multiply 3-digit by 1-digit number

Now, let’s try it with a bigger number. Let’s multiply a three-digit number by a one-digit number.
Multiply 3 x 245.
First, breakdown 245 as 2 hundreds 4 tens and 5 ones. 245 = 200 + 40 + 5
Then, draw a rectangle and split the rectangle into three so that each part is slightly bigger or smaller than the others. Label each part as 200, 40, and 5 where the smaller part of the rectangle is labeled 5.
Label the left side of the rectangle as 3.
Now, multiply the hundreds and write the product inside the cell directly underneath 200.
2 hundreds x 3 or 200 x 3 = 600
Next, multiply the tens and write the product inside the cell underneath 40.
4 tens x 3 or 40 x 3 = 120
Then, multiply the ones and write the product inside the cell underneath 5.
5 ones x 3 or 5 x 3 = 15
Lastly, add the products.
600 + 120 + 15 = 735
So, the product of 3 x 245 is 735.
Multiply 4-digit by 1-digit
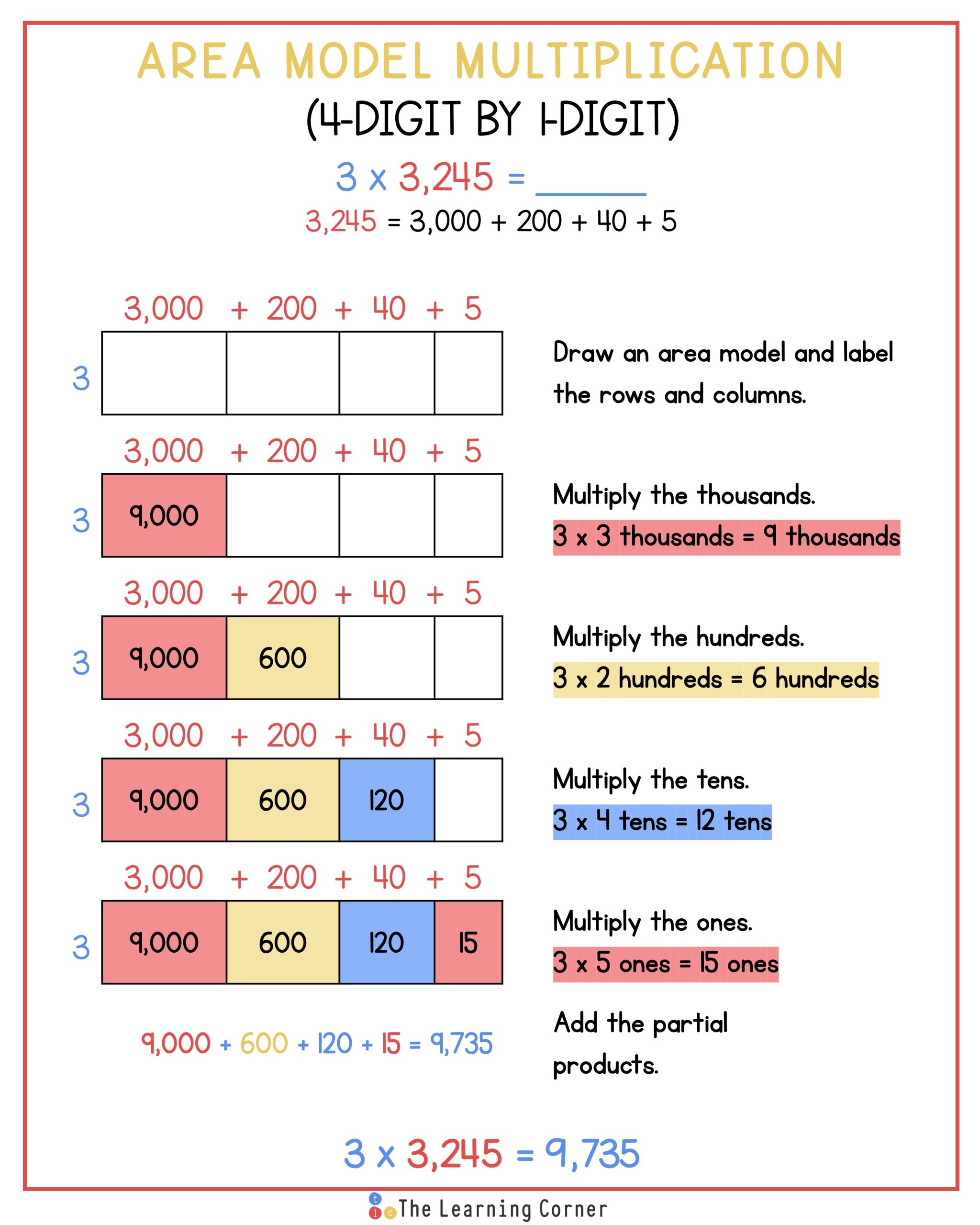
Area models can also be used to multiply 4-digit by 1-digit numbers. Let’s do an example for 3 x 3,245.
First, breakdown the bigger number, which is 3,245, as 3 thousands, 2 hundreds, 4 tens, and 5 ones.
Then, draw a rectangle and split the rectangle into four parts so that each digit of the factors can be represented in the area model. Label the first column 3,000; the second column 200; the third column 40; and the last column 5. Next, label the left side of the rectangle 3.
Now, multiply the thousands and write the product inside the cell directly underneath the column for the thousands place.
3 thousands x 3 or 3,000 x 3 = 9,000
Then, multiply the hundreds and write the product inside the cell directly underneath the column for the hundreds place.
2 hundreds x 3 = 200 x 3 = 600
Next, multiply the tens and write the product inside the cell directly underneath the cell for the tens place.
4 tens x 3 or 40 x 3 = 120
Then, multiply the ones and write the product directly underneath the cell for the ones place.
5 ones x 3 or 5 x 3 = 15
Lastly, add the product.
9,000 + 600 + 120 + 15 = 9,735
So the product of 3 x 3,245 is 9,735.
Area Model Multiplication: 2-Digit by 2-Digit Numbers
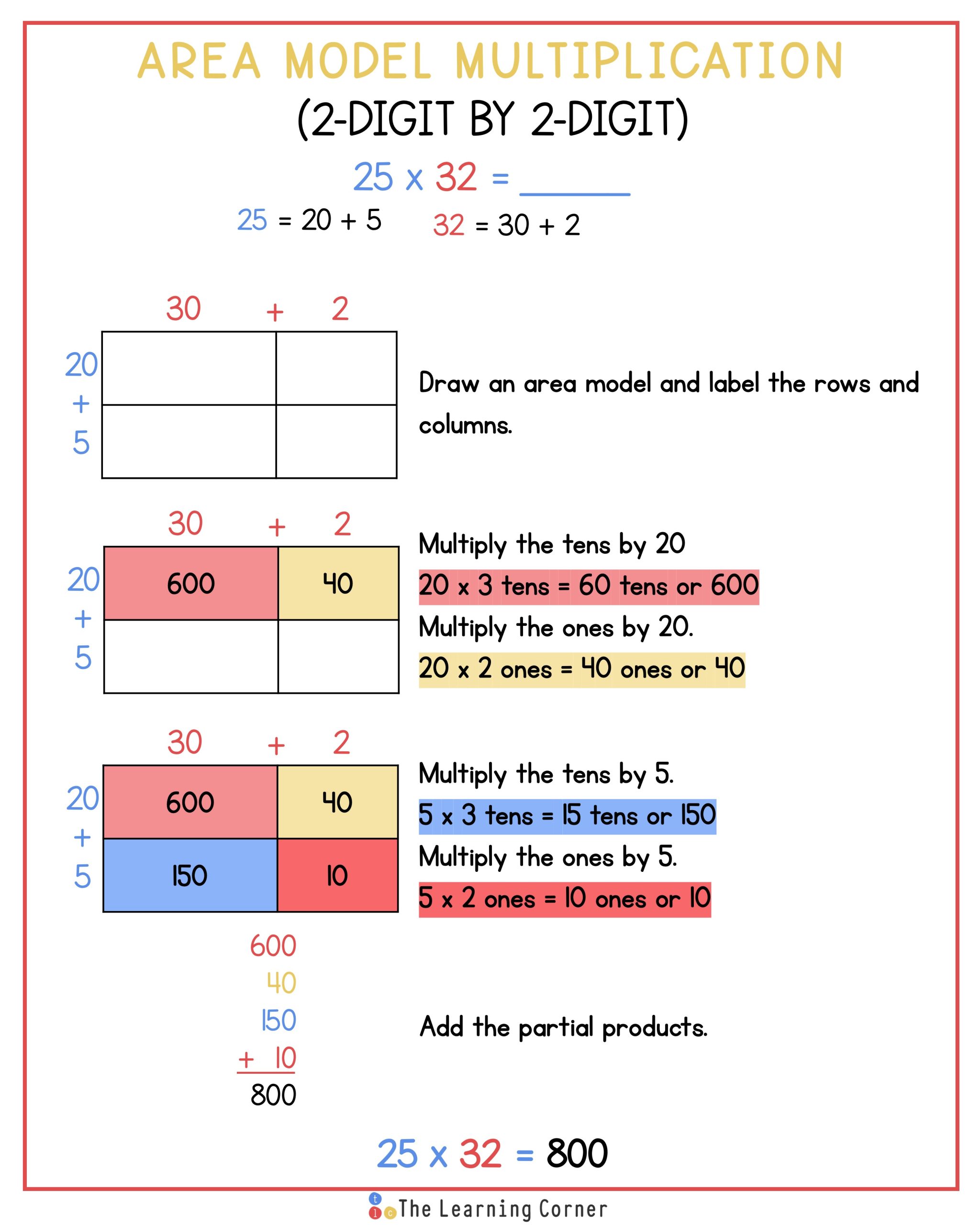
Area model multiplication is also great when multiplying 2-digit by 2-digit numbers. Again, it is important to break down both factors. Let’s try it with an example.
Multiply 25 x 32. Break down both factors so that they show tens and ones.
25 = 2 tens 5 ones or 20 + 5
32 = 3 tens 2 ones or 30 + 2
Now, draw an area model that has two columns and two rows. Label the columns 20 and 5, and label the rows 30 and 2.
Start multiplying. This area model works like a multiplication table, the products of the rows and columns are written where they meet.
First, multiply 2 tens by 3 tens. Make sure to write the product where they meet, the top left cell of the area model.
20 x 30 = 600
Then, multiply 5 ones by 3 tens. Write the product where they meet, the top right cell.
5 x 30 = 150
Next, multiply 2 tens by 2 ones. Write the product where they meet, the bottom left cell.
20 x 2 = 40
Then, multiply 5 ones by 2 ones. Write the product where they meet, the bottom right cell.
5 x 2 = 10
Lastly, add the products. Making sure to align the place value of the digits.
600 + 150 + 40 + 10 = 800
So, the product of 25 x 32 is 800.
That’s how you multiply 2-digit numbers by 2-digit numbers using an area model.
Benefits of Using an Area Model
Now, why do area model multiplication when it is faster to multiply using the standard algorithm? Let me tell you why. Multiplying using the standard algorithm may be more efficient, but using area models when multiplying will give you a better understanding of the multiplication process. Not only that, but it also breaks down the numbers (especially big ones!) into smaller chunks so that it is easier to multiply. Another thing I love about area model multiplication is that it is easier to visualize the place value of each digit, thus giving a better understanding of the multiplication process!
Ways to Practice Multiplying Using Area Models
There are several ways to practice multiplying using area models. Here are some of my favorites.
- Use lapboards and different colored markers to show multiplication. This can help further visualize how to multiply the numbers.
- Use digital tools such as Google Slides™. I love using Google Slides™ with my students, especially for quick practice. The activities are interactive with drag-and-drop options, making it much easier for your students to understand multiplying using area models. Here are some of my favorite products.
- Use guided notes to help break down the process of multiplying using area models even more.
- Use area models practice worksheets that help differentiate and visualize multiplication. When introducing a new topic to my students, I love sending them packets to work on and practice so that they are more confident with the skill or topic. Here are my favorite packets for area model multiplication!
Are you looking for ways to teach multiplication effectively? Check out this blog post!








