Adding and subtracting fractions are two operations that combine or take away part of a given fraction. In this article, we will show you a step-by-step guide on how to add and subtract fractions with like denominators. There are different ways to add and subtract fractions.
- Using Models
- Using Fraction strips
- Computation
USE MODELS TO ADD AND SUBTRACT FRACTIONS
Models represent what is given in the real world. This method of adding and subtracting fractions is best used
Adding fractions with like denominators using a model
When given a word problem to add fractions, start with a model. Here are the steps when adding fractions using a model.
- Draw a model to show the whole fraction.
- Shade the model to show the first addend.
- Shade the same model to show the second addend.
- Count the number of shaded parts.
Below is an example problem to solve adding fractions.

For Jacob’s birthday, his mom bought a cake and sliced it into twelfths. Jacob and his friends ate four-twelfths of the cake while the adults ate three-twelfths of the cake. What fraction of the cake was eaten on Jacob’s birthday?
Step 1: Model the problem by drawing a circle. This represents the cake. Draw lines on the circle to show that there are twelve slices.
Step 2: Shade the part of the circle to show how much Jacob and his friends ate. (Shade 4 out of 12)
Step 3: Shade the part of the circle to show how much cake the adults ate. (Shade 3 out of 12)
Step 4: Count how many slices are shaded. (7 out of 12)
Quick note: Fractions are written with a numerator and a denominator. The numerator is the part that tells how many we are counting and the denominator tells how many parts there are in total.
Step 5: Write the fraction to represent the total amount of cake that was eaten. Write 7 for the numerator and 12 for the denominator.
So, 7⁄12 of Jacob’s cake was eaten on his birthday.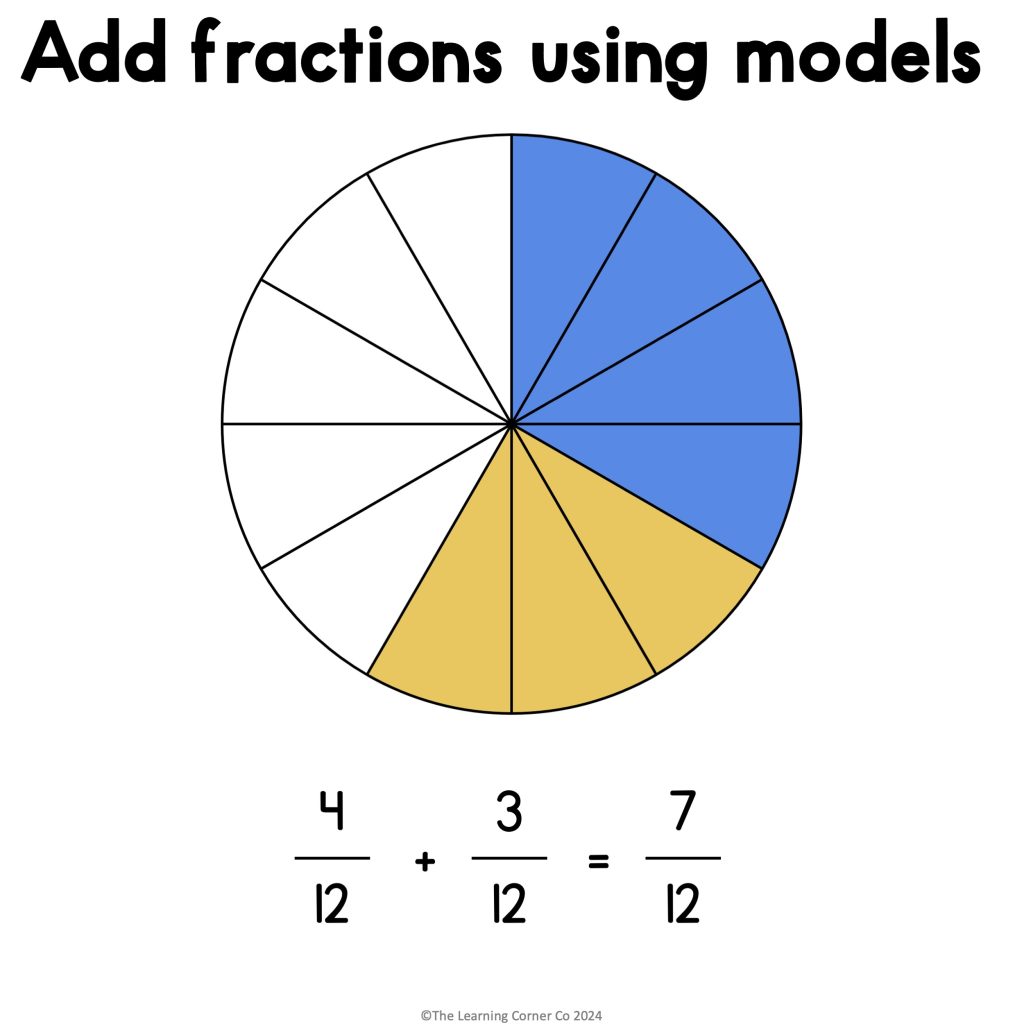

✅ Step-by-step guided notes to break down tricky concepts.
✅ Visual models and plenty of practice for confidence-building.
✅ Review pages and answer keys for extra support.
Perfect for homework, tutoring, or classroom use, this workbook is ideal for kids ages 9-12. Grab your copy today and make fractions a breeze! ✨
Subtracting fractions with like denominators using a model
Models are also helpful when subtracting fractions too. In order to subtract fractions using a model, follow these steps.
- Draw a model to show the whole fraction.
- Model the minuend.
- Cross out the subtrahend.
- Count the number of leftover parts.
- Write the fraction that represents the model.
To give an example, look at the word problem below.

Mr. Co has three-fourths yard of fabric. He made a throw pillow cover and used two-fourths yard of fabric. How much fabric is left?
Step 1: Model the problem by drawing a rectangle. Draw vertical lines on the rectangle to show fourths.
Step 2: Shade three parts to show how much fabric Mr. Co has.
Step 3: Since Mr. Co used two-fourths yards of fabric, cross out two of the shaded parts.
Step 4: Count how many parts are shaded and not crossed out. (1 out of 4)
Step 5: Write the fraction representing what part of the fabric is left. (¼)
So, Mr. Co has 1⁄4 yard of fabric left.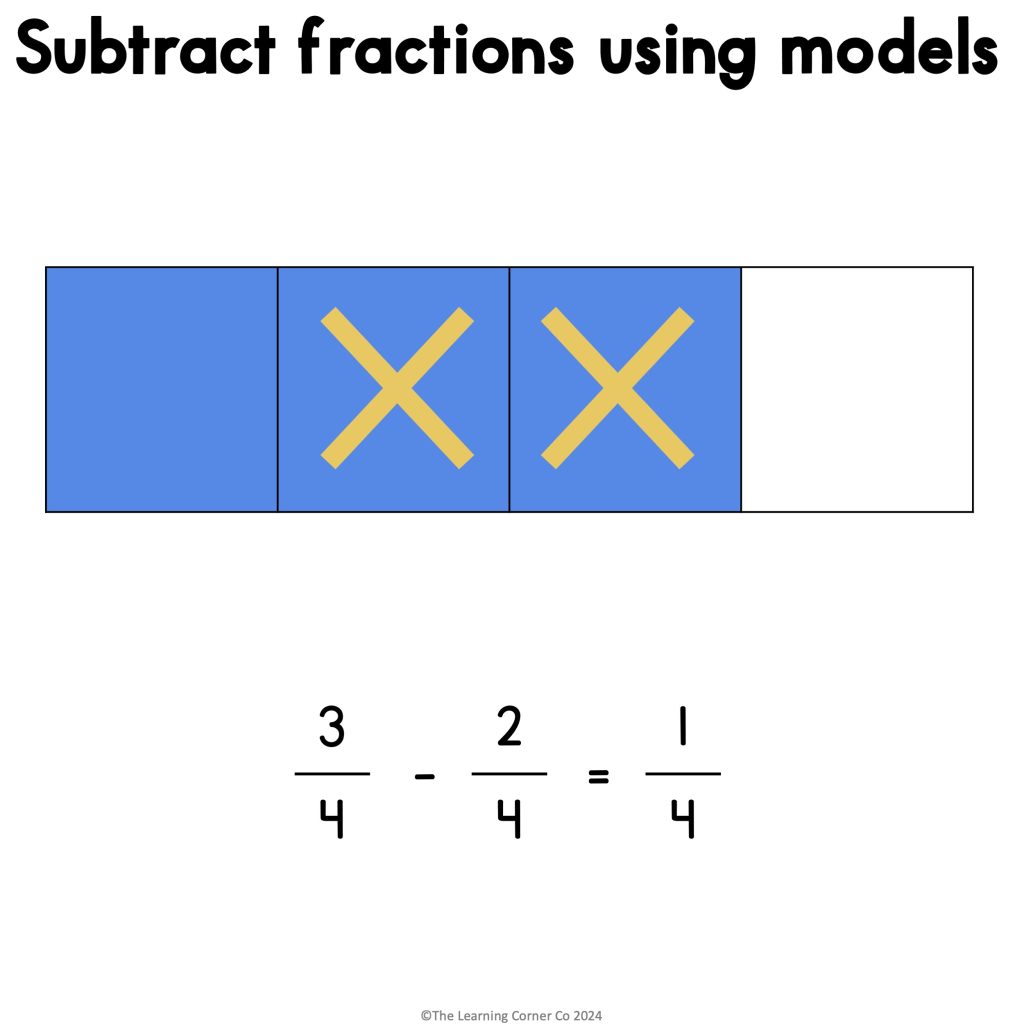
USE FRACTION STRIPS TO ADD AND SUBTRACT FRACTIONS
Fraction strips represent a whole in different ways. You can break them up into parts or combine them. These can be folded or cut depending on your needs. These work great to model adding and subtracting fractions.
Adding fractions using fraction strips
When using fraction strips to add fractions, you can model both addends using the strips. Let’s solve the example below.
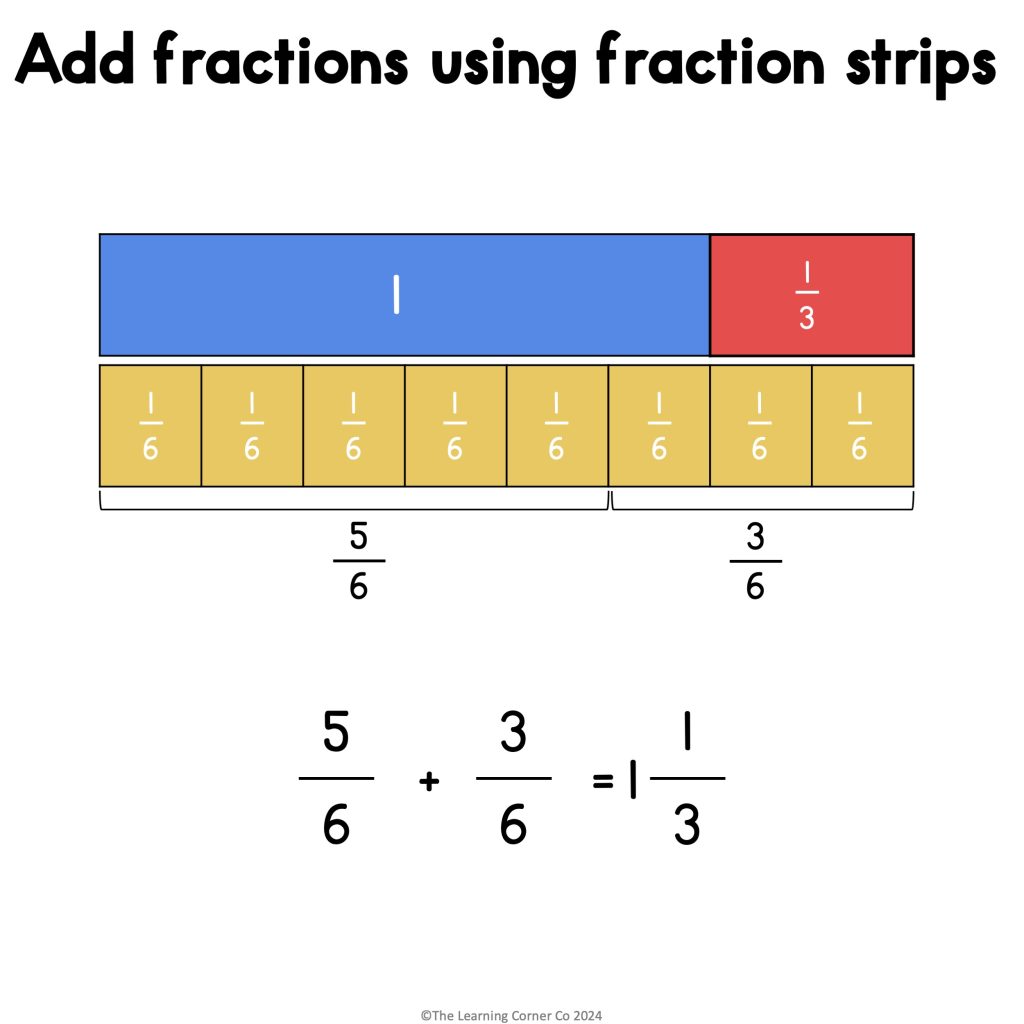
Step 1: Model one whole to have a benchmark for the sum.
Step 2: Just below the one whole strip, place five-sixths.
Step 3: Beside the five-sixth strips, place three-sixths.
Step 4: Count the number of sixth-size strips that you have. You’ll notice that it is more than one whole since the sume is longer than the one whole strip.
Step 5: Write the sum as a mixed number. You have one whole and two-sixth strips.
Step 6: Simplify the fraction. You can also use the fraction strips. Look for a fraction strip that has the same size as two-sixths. In this case, it is one-third.
5⁄6 + 3⁄6 = 1 1⁄3Subtracting fractions using fraction strips
When using fraction strips to subtract fractions, model the minuend then cross out the subtrahend. Let’s solve the example below.
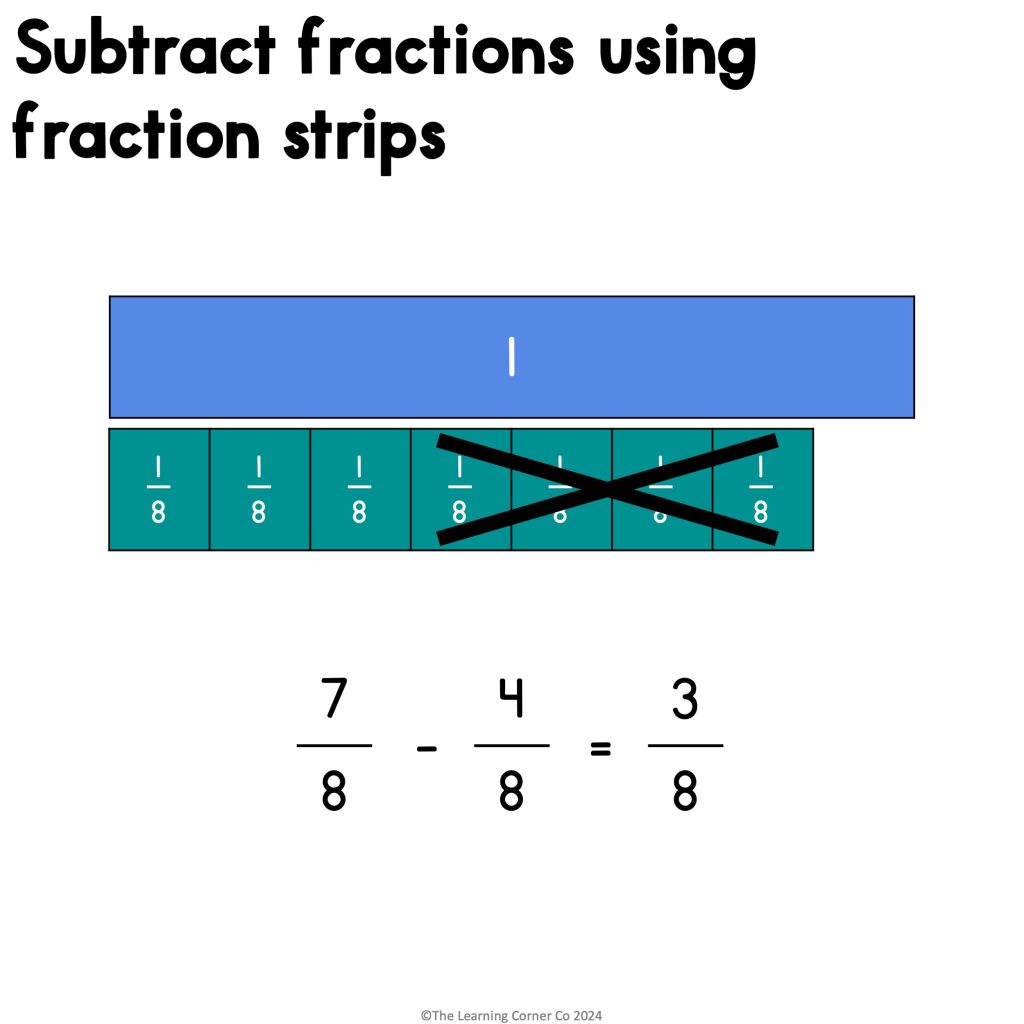
Step 1: Model the subtrahend seven-eighth.
Step 2: Cross out the subtrahend four-eighth.
Step 3: Count the number of strips left. There are three-eighths.
7⁄8 – 3⁄8 = 1⁄2USE COMPUTATION TO ADD AND SUBTRACT FRACTIONS
When adding and subtracting fractions, you can directly add or subtract the numerators and keep the denominator common.
Follow the steps below when adding or subtracting fractions:
Step 1: Add or subtract the numerators.
Step 2: Keep the common denominator.
Step 3: Simplify the fraction.
Let’s see the examples below.
Example 1: Adding fractions with like denominators
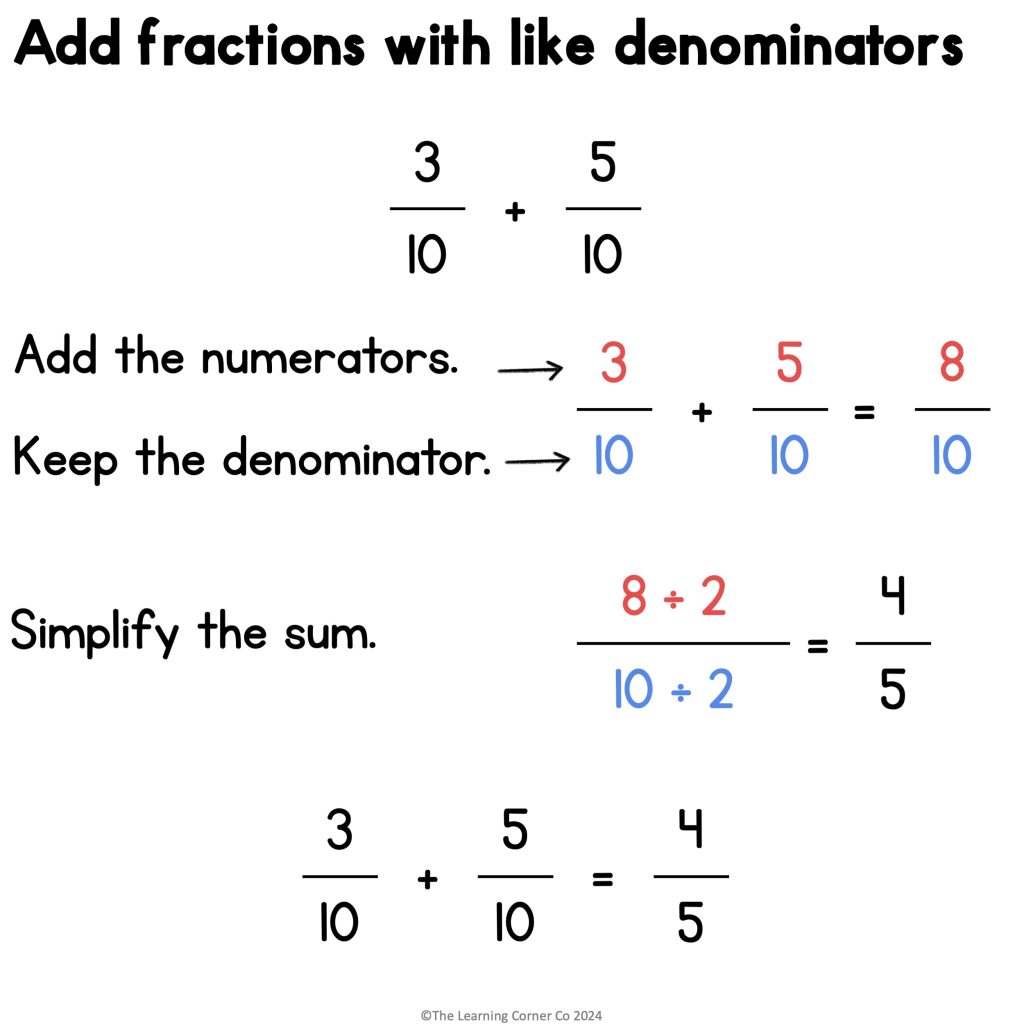
First, check that the denominators are the same. Both of them have 10 as their denominators.
Since the denominators are the same, you can directly add the numerators.
3 + 5 = 8
Then, keep the denominator 10.
3⁄10 + 5⁄10 = 8⁄10Check that the numerator and denominator do not have a common factor. Since eight and ten have a common factor of 2, simplify the fraction.
Divide the numerator and the denominator by 2.
8÷2⁄10÷2 = 4⁄5 So, 3⁄10 + 5⁄10 = 4⁄5Example 2: Subtracting fractions with like denominators
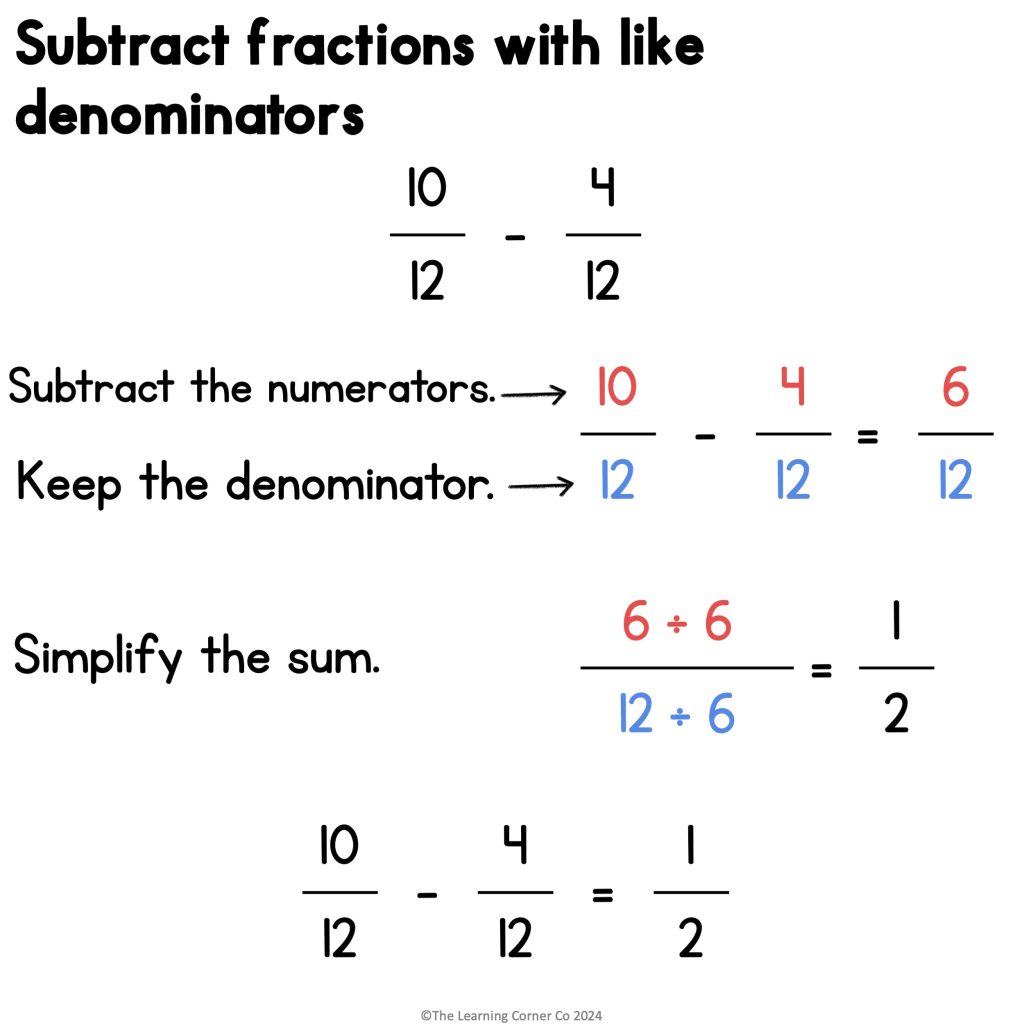
Check that the denominators are the same. Both of them have 12 as their denominators.
Since the denominators are the same, you can directly subtract the numerators.
10 – 4 = 6
Then, keep the denominator 12.
10⁄12 – 4⁄12 = 6⁄12Check that the numerator and denominator do not have a common factor. Since 6 and 12 have a common factor of 6, you need to simplify the fraction.
Divide the numerator and denominator by 6.
6÷6⁄12÷6 = 1⁄2 10⁄12 – 4⁄12 = 1⁄2Adding and subtracting fractions worksheet
With fractions (or any other math topic), practice plays a huge role in student’s understanding and confidence in the topic. Check out the links below if you are looking for worksheets with answer keys and guided notes.
FAQ
1. Add the numerators.
2. Keep the common denominators.
3. Simplify the fraction.
1. Subtract the numerators.
2. Keep the common denominators.
3. Simplify the fraction.
1. Find the greatest common factor of the numerator and the denominator.
2. Divide the numerator and the denominator by the greatest common factor.







