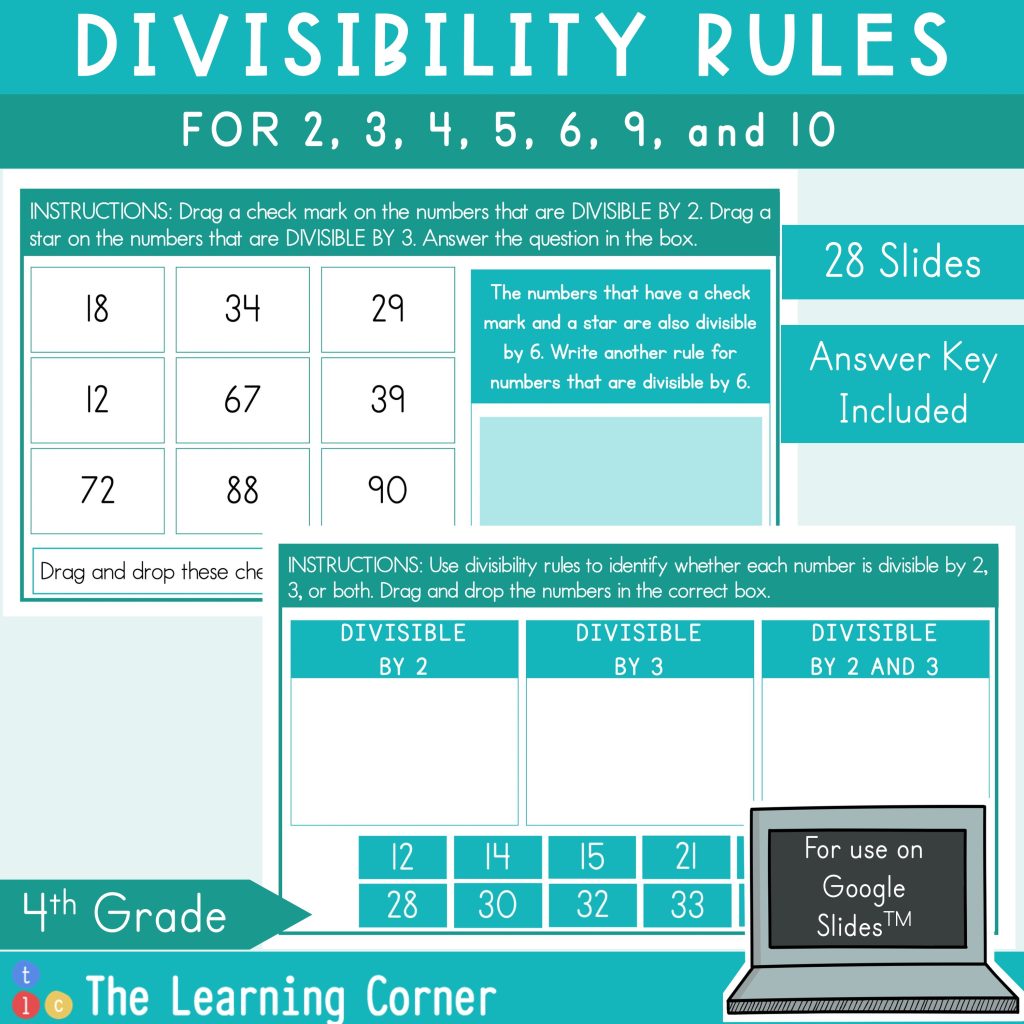
Do you also teach divisibility rules? It is a tricky concept to grasp especially the first time it is introduced. Sure, knowing their division facts is pretty easy, but when it comes to dividing big numbers, these rules come in handy.
What I love to do with my students is to give them tons of examples to test the rules. After, I give them a guide they can always refer to. Aside from that, I also find that having a lot of examples of what is and what is not divisible by a given number is helpful and gives them confidence in the topic.
Divisibility rules are just one of those topics that is a struggle to introduce, but with constant practice, my students understand it too.
Often, they don’t see the significance of divisibility rules so I show them how it can be used with other topics. This helps them to appreciate divisibility rules, especially with other math concepts that we’ve already covered.

Why do you need to know the rules of divisibility?
Several math topics will be so much easier when students apply their knowledge of divisibility rules.
- Prime factorization – When determining the prime factorization of a big number, divisibility rules come in handy. Just by knowing what the number is divisible by can be very helpful.
- GCF – Since division is the opposite of multiplication, knowing the divisibility rules will help your students figure out the greatest common factor of a given set of numbers.
- Factoring – This may not be an elementary concept. However, the more practice with divisibility rules your students know, the easier it is for them to factor a number. Their number fluency improves and they will be able to easily factor out a number.
“But teacher, we don’t even use math every day,” that is pretty much a phrase I often hear my students. So, other than applying divisibility rules to other math concepts, let your students know that it can also be used in everyday life situations.
An example of using divisibility rules is at a grocery store. Figuring out the best deal is so much easier, and you don’t even have to do a whole division problem. Oftentimes, my students need a little reminder on how to use a concept in everyday life to keep them motivated to learn it.
What are the rules of divisibility?
If you are teaching divisibility rules right now, then these are the rules and some examples.

2: If a number’s last digit is 0, 2, 4, 6, or 8 then a number is divisible by 2.
- Example: The last digit of the number 574 is 4, so it is divisible by 2.

3: If the sum of the digits is a multiple of 3 (3, 6, 9, 12, 15, 18, 21…) then a number is divisible by 3.
- Example: You have the number 681. The sum of the digits 6 + 8 + 1 is 15. 15 is a multiple of 3 so it is divisible by 3.

4: If the last two digits of a number are a multiple of 4 (4, 8, 12, 16, 20, 24, 28 …) then a number is divisible by 4.
- Example: You have the number 532. The last two digits of the number is 32. 32 is a multiple of 4. So, 532 is a divisible by 4.

5: If a number’s last digit is 5 or 0, then it is divisible by 5.
- Example: The number is 890. It ends in 0. This means that 890 is divisible by 5.

6: If a number is divisible by 2 and 3, then it is divisible by 6.
- Example: A number is 468. Its last digit is 8, so it is divisible by 2. Now, check if it is divisible by 3. The sum of the digits 4 + 6 + 8 is 18. 18 is a multiple of 3. This makes 468 divisible by 2 and 3. This means that it is also divisible by 6.

9: If the sum of the digits is a multiple of 9 (9, 18, 27, 36, 45, …) then it is divisible by 9.
- Example: The number is 972. The sum of the digits 9 + 7 + 2 is 18. 18 is a multiple of 9. This means that 972 is divisible by 9.

10: If a number’s last digit is 0, then it is divisible by 10.
- Example: The last digit of 740 is 0. This means that it is divisible by 10.
Worksheets and Activities
If you are looking to review divisibility rules with your students. Check out this divisibility rules worksheet. It provides plenty of examples for your students to try and master the rules.
Here are other digital resources and activities that you may find helpful.
Need more help with division? Check out this blog post about area model division.