Are you finding it difficult to find common denominators in fractions? Writing fractions with common denominators are necessary when comparing, adding, and subtracting fractions. There are two ways to find common denominators. One is by using least common multiples and another one is by using multiplication.
How do you find common denominators using least common multiples?
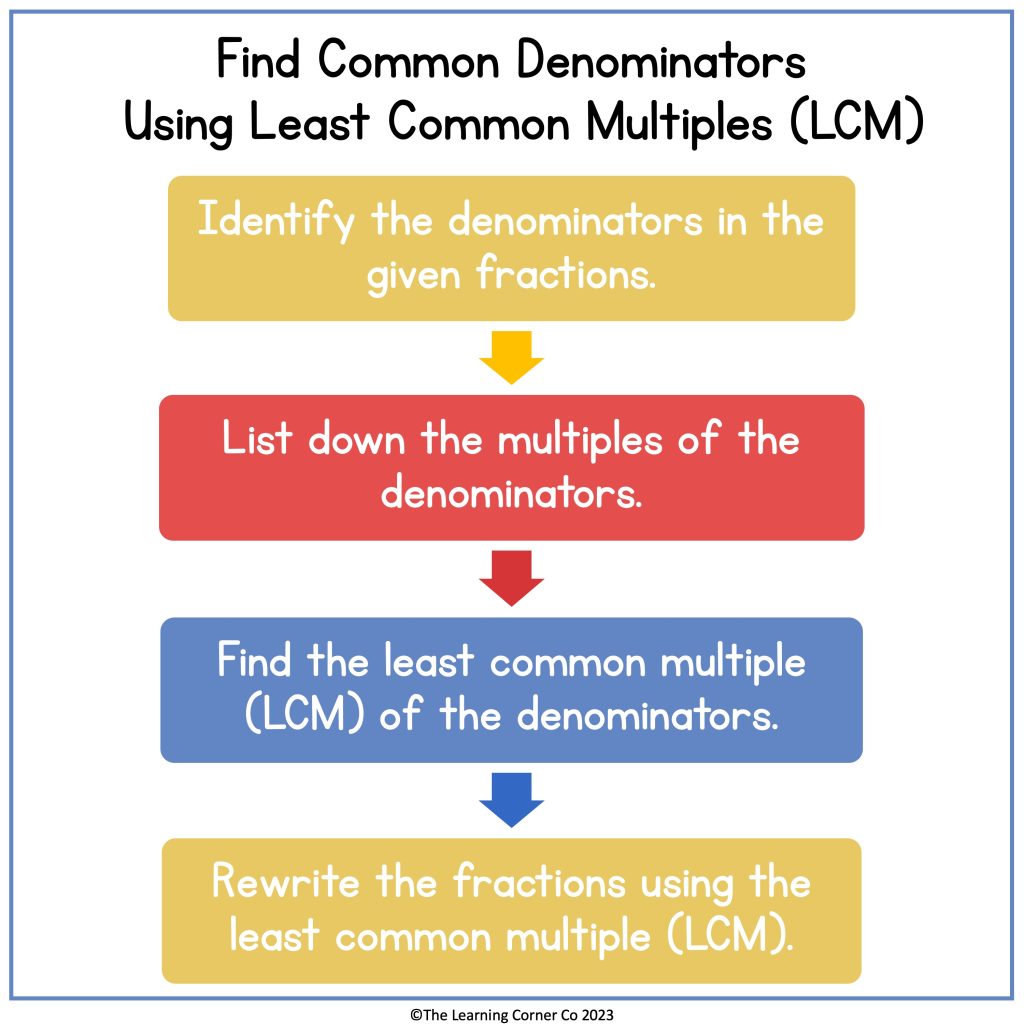
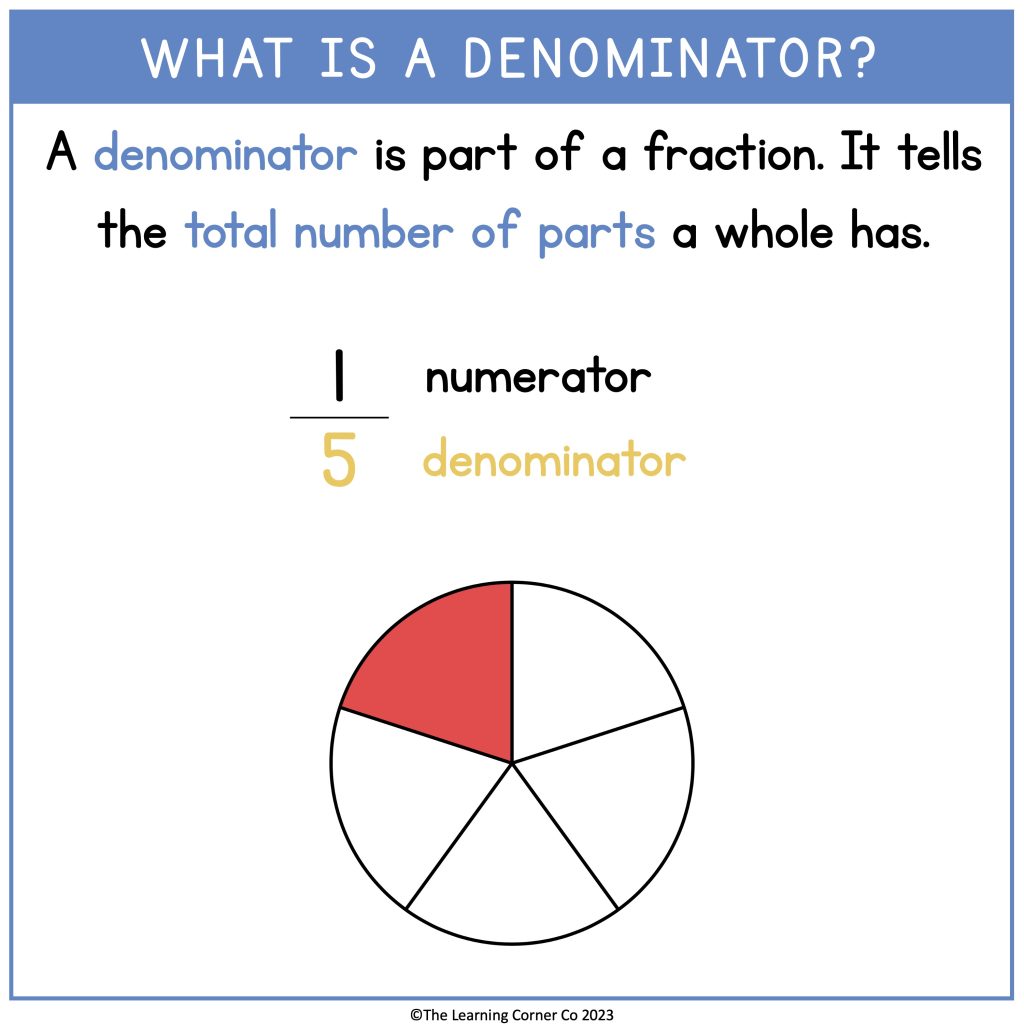
- Identify the denominators in the given fraction. A denominator is the bottom number of a fraction. It represents the total number of equal parts in a whole.
- List the multiples of the denominators. Start with the first five multiples and keep on listing until you find a common multiple.

- Find the least common multiple (LCM) of the given fractions. A common multiple is a multiple of both denominators. It means they are sharing the same multiple. Once there is a common multiple, use the least and use that multiple as your new denominator.
- Rewrite each fraction using the LCM as a common denominator. Using the least common multiple, write new numerators. To find the new numerators, divide the LCM by the given denominators. Use the quotient to multiply by the old numerator. The product is your new numerator. Rewrite the new fractions.
Here’s an example. Let’s rewrite one-half and two-thirds so that they have a common denominator.
First, identify the denominators. The denominators are 2 and 3.
Next, list down the multiples of 2 and 3. Let’s start with the first five multiples.
- Multiples of 2: 2, 4, 6, 8, 10
- Multiples of 3: 3, 6, 9, 12, 15

Then, look for the least common multiple (LCM). Notice on your list that both 2 and 3 have 6 as their common multiple and it’s also the least. So, use 6 as your new denominator.
Now, let’s rewrite each fraction using the LCM as the new denominator.
Rewrite ½ (one-half). First, divide 6 by 2, since 2 is the old denominator. 6 ÷ 2 = 3. Multiply 3 by the old numerator, which is 1. So, 3 x 1 = 3. Use 3 as your new numerator. That means that ½ = 3/6 (one-half equals three-sixths).
Now, let’s rewrite 2/3. First, divide 6 by 3, since 3 is the old denominator. So, 6 ÷ 3 = 2. Then, multiply 2 by the old numerator, which is 2. So, 2 x 2 = 4. Use 4 as your new numerator. That means that 2/3 = 4/6 (two-thirds equals four-sixths).


Are you looking to help your 4th grader learn fractions? This Fractions Workbook is jam-packed with worksheets and notes to help your students understand and master fractions.
Four topics are covered to support learning fractions.
- Equivalent Fractions
- Simplify Fractions
- Find Common Denominators
- Compare and Order Fractions
How to find common denominators using multiplication?
Another way to write fractions with common denominators is by multiplying. Multiply the numerator and the denominator of the given fraction to the denominator of the other fraction.
Here’s an example. Let’s rewrite three-fifths and four-ninths so they have a common denominator.
- To rewrite 3/5, multiply the numerator and denominator by 9. So, the new fraction is 27/45.
- To rewrite 4/9, multiply the numerator and denominator by 5. So, the new fraction is 20/45

Activities to practice the skill
- Roll two six-sided die twice. The first roll is your first fraction, and the second roll is your second fraction. Rewrite the two fractions with common denominators.
- Have a deck of cards without the face cards. (You may also assign the face card numbers such as 11 for Jack, 12 for Queen, and 13 for King.) Pull two cards to make one fraction. Pull two more to make another fraction. Using those two fractions, rewrite the two fractions with common denominators.
- Practice finding common denominators using worksheets and templates. Here are some worksheets that you may like. (These links will bring you to my TPT store.)
To recap, common denominators are important when comparing, adding, and subtracting fractions. When finding common denominators, it is important to find the least common multiple (LCM) and using it as the common denominator. Continue practicing by doing a variety of activities to help you with the skill.







